Parcours de graphe

Objectifs

• Définir le parcours d'un graphe
• Différencier les parcours en profondeur et en largeur
• Définir, différencier et utiliser une pile et une file
• Appliquer un parcours en profondeur et en largeur à un graphe

Cours

Parcours de graphe

Graphes

Parcours d'arbre

• Problème : Visiter tous les sommets d'un arbre.

• Solution : Application d'un algorithme de parcours

• Ordres possibles :

  • Parcours en largeur : Breadth-First Search (BFS)

  • Parcours en profondeur : Depth-First Search (DFS)

Parcours en largeur (BFS)

https://commons.wikimedia.org/wiki/File:Breadth-First-Search-Algorithm.gif

Parcours en profondeur (DFS)

https://commons.wikimedia.org/wiki/File:Depth-First-Search.gif

BFS vs DFS

https://www.freelancinggig.com/blog/2019/02/06/what-is-the-difference-between-bfs-and-dfs-algorithms/

Depth and Breadth

https://xkcd.com/2407

• Problème : Visiter tous les sommets d'un graphe (généralisation de l'arbre).

• Différence : Cycle ou circuit possible.

• Solution : Garder en mémoire les sommets déjà visités.

Structures de données

• Pile (stack) : LIFO (Last In First Out)

• File (queue) : FIFO (First In First Out)

Pile

https://waytolearnx.com/2019/03/difference-entre-pile-et-file-dans-la-structure-des-donnees.html

File

https://waytolearnx.com/2019/03/difference-entre-pile-et-file-dans-la-structure-des-donnees.html

Exercice : Pile ou file ?

• Historique de navigation

  • Pile

• Numéros d'attente au guichet

  • File

• La fonction annuler (ctrl + z)

  • Pile

• Liste d'impression

  • File

Exercice : Pile

• Lire les symboles de gauche à droite

  • Lettre : empiler

  • * : dépiler et afficher

• A B C * *

  • CB

• U B * L * E * *

  • BLEU

Notation polonaise inverse

• Opérande (nombre ou variable) : empiler

• Opérateur : dépiler les deux derniers, effectuer l'opération, puis empiler le résultat

• Avantage : pas besoin de parenthèses

https://commons.wikimedia.org/wiki/File:CPT-RPN-example1.svg

Parcours en profondeur (DFS)

https://www.programiz.com/dsa/graph-dfs

Initialiser avec une pile vide.

Parcours en profondeur (DFS)

https://www.programiz.com/dsa/graph-dfs

Visiter 0 et empiler les voisins.

Parcours en profondeur (DFS)

https://www.programiz.com/dsa/graph-dfs

Dépiler 1 (pas de nouveaux voisins).

Parcours en profondeur (DFS)

https://www.programiz.com/dsa/graph-dfs

Dépiler 2 et empiler ses voisins.

Parcours en profondeur (DFS)

https://www.programiz.com/dsa/graph-dfs

Dépiler 4 (pas de nouveaux voisins).

Parcours en profondeur (DFS)

https://www.programiz.com/dsa/graph-dfs

Dépiler 3 et fin car la pile est vide.

Parcours en profondeur (DFS)

• Que représente la pile ?

  • Liste des sommets découverts à visiter.

Parcours en largeur (BFS)

https://www.programiz.com/dsa/graph-bfs

Initialiser avec une file vide.

Parcours en largeur (BFS)

https://www.programiz.com/dsa/graph-bfs

Visiter 0 et enfiler les voisins.

Parcours en largeur (BFS)

https://www.programiz.com/dsa/graph-bfs

Défiler 1 (pas de nouveaux voisins).

Parcours en largeur (BFS)

https://www.programiz.com/dsa/graph-bfs

Défiler 2 et enfiler ses voisins.

Parcours en largeur (BFS)

https://www.programiz.com/dsa/graph-bfs

Défiler 3 (pas de nouveaux voisins).

Parcours en largeur (BFS)

https://www.programiz.com/dsa/graph-bfs

Défiler 4 et fin car la file est vide.

Parcours en largeur (BFS)

• Que représente la file ?

  • Liste des sommets découverts à visiter.

DFS

https://xkcd.arnaud.at/761

Exercice

L'ordre d'habillement suivant est-il DFS ou BFS ?

1. Sous-vêtements

2. T-shirt

3. Pull

4. Collants

5. Pantalon

6. Chaussettes

7. Chaussures

DFS : on fait tout le haut, puis tout le bas, ...

Exercice

Quel serait l'ordre en BFS en commençant par les sous-vêtements ? (Chaussettes, Chaussures, Collants, Pantalon, Pull, T-shirt)

1. Sous-vêtements

2. T-shirt

3. Collants

4. Chaussettes

5. Pull

6. Pantalon

7. Chaussures

Exercice

Graphe de dépendances en commençant par les sous-vêtements ? ? (Chaussettes, Chaussures, Collants, Pantalon, Pull, T-shirt)

F pour passer en plein écran ou O pour afficher la vue d'ensemble.
Versions sans animation, plein écran, imprimable.

Exercices

Pile

Lire les symboles de gauche à droite :

• Lettre : empiler
• * : dépiler

1. I N V O * * * *
2. V * R E * * T *
3. L E B * U L * * *
4. E L B * U * L * * *

Solution

1. I N V O * * * * : O V N I
2. V * R E * * T * : V E R T
3. L E B * U L * * * : B L U E
4. E L B * U * L * * * : B U L L E

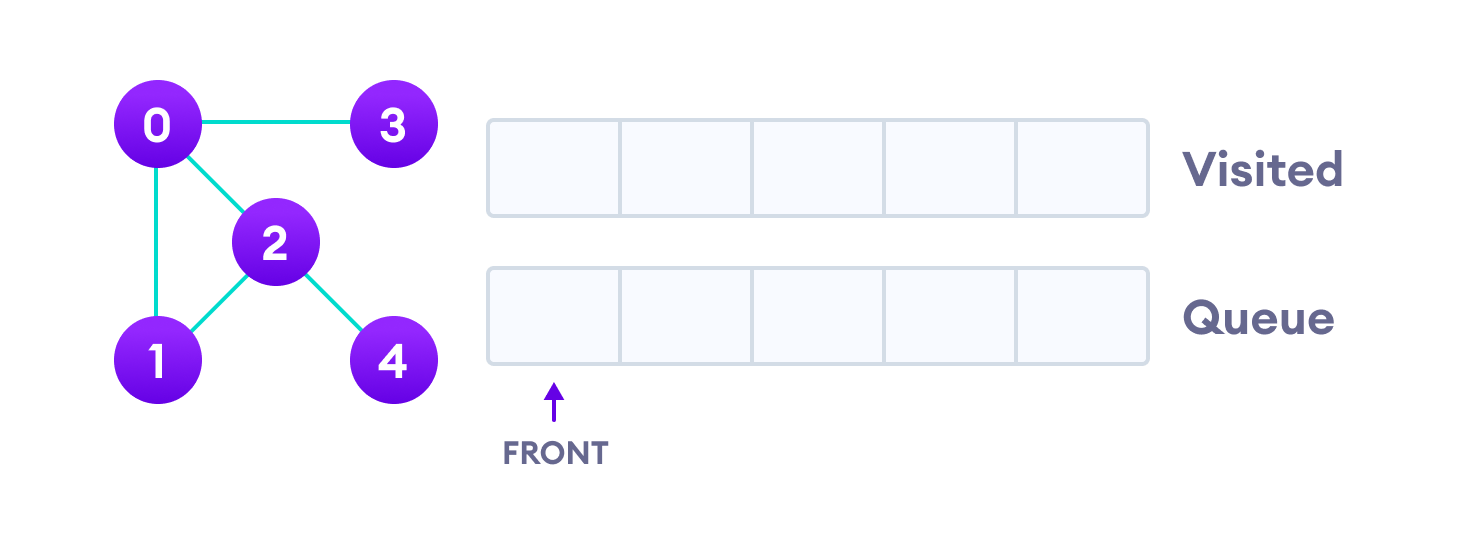
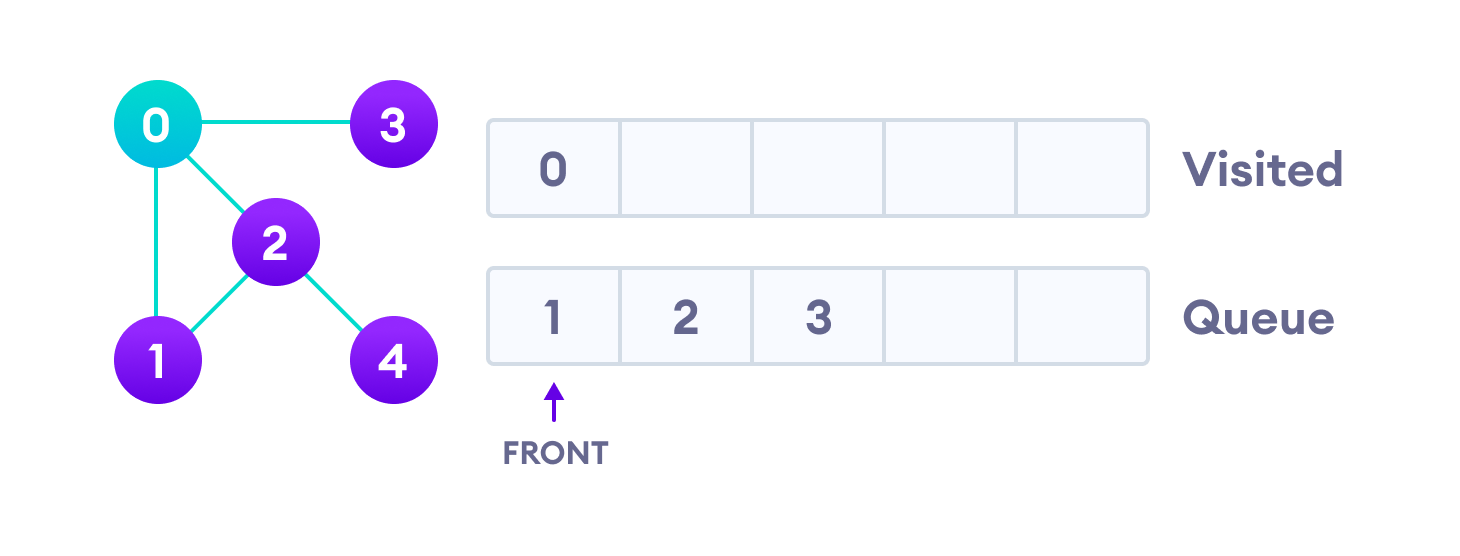
File

Lire les symboles de gauche à droite :

• Lettre : enfiler
• * : défiler

1. I N V O * * * *
2. V * R E * * T *

Solution

1. I N V O * * * * : I N V O
2. V * R E * * T * : V R E T

L'ordre est préservé : FIFO (First In First Out)

Parcours d'arbre

Quelle est l'ordre de parcours de l'arbre suivant en commençant par bleu ?

1. Parcours en profondeur (DFS)
2. Parcours en largeur (BFS)

Solution

Réponses possibles :

1. bleu - rouge - jaune - turquoise - orange - vert - noir
2. bleu - rouge - vert - jaune - turquoise - noir - orange

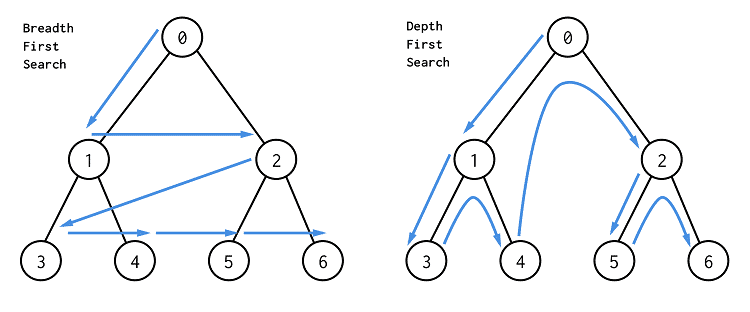
Parcours de graphe

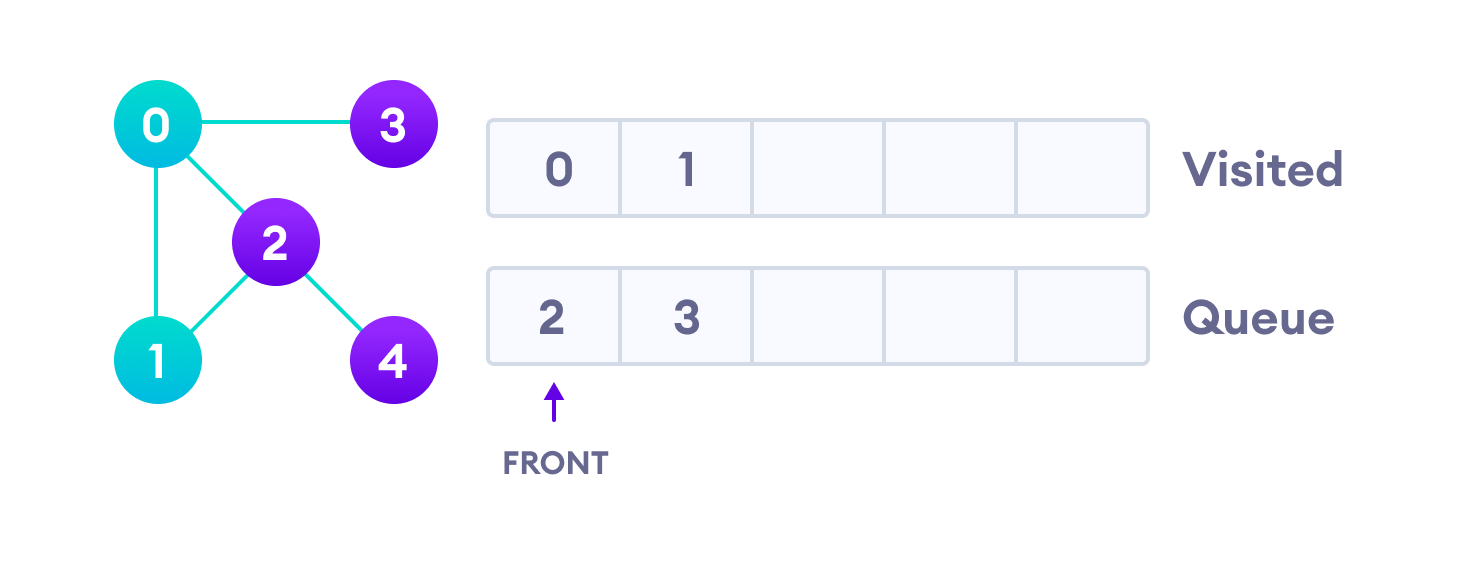
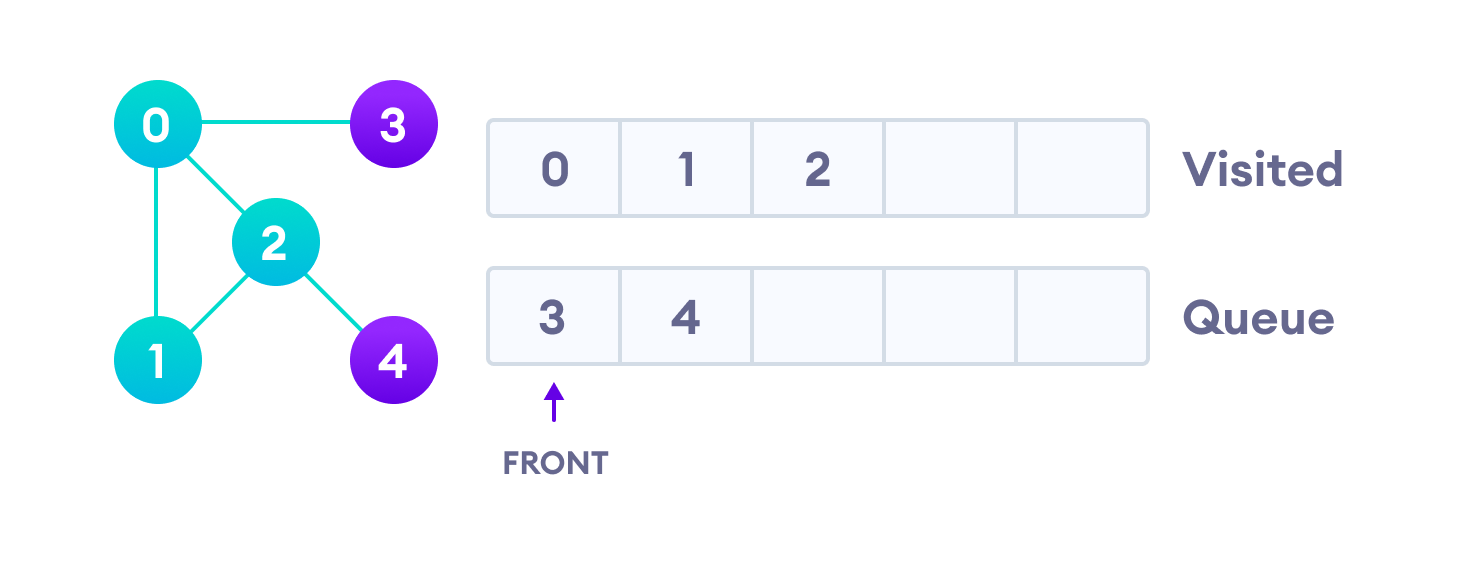
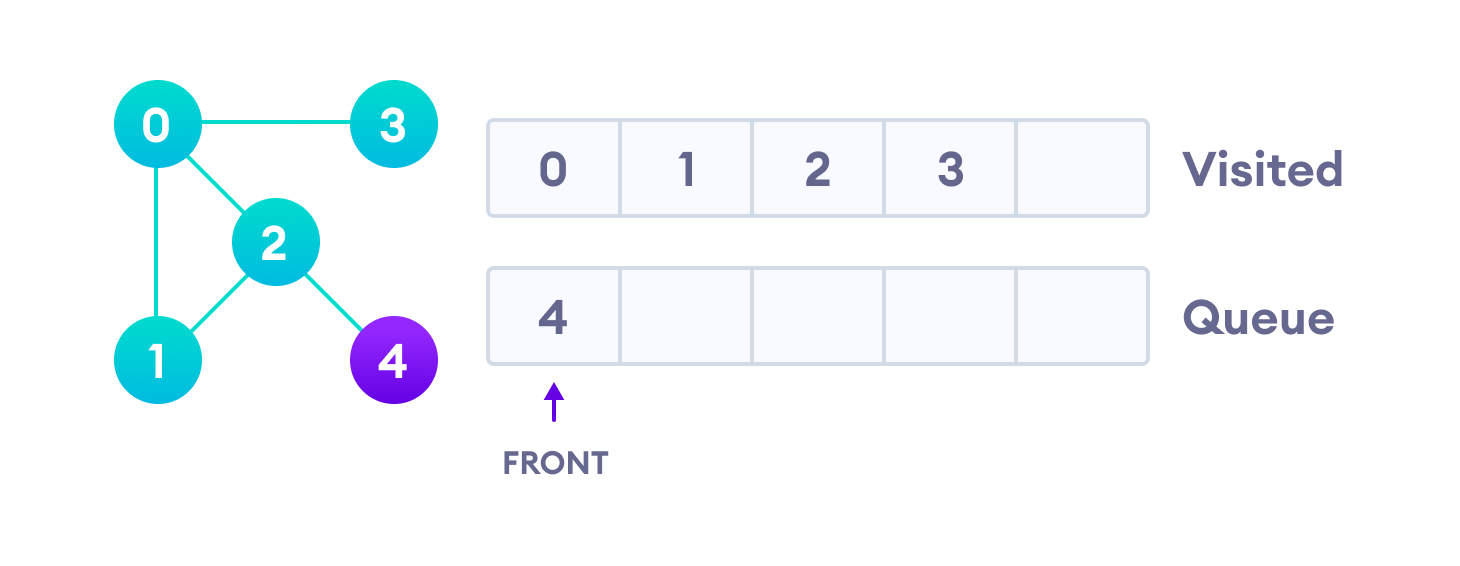
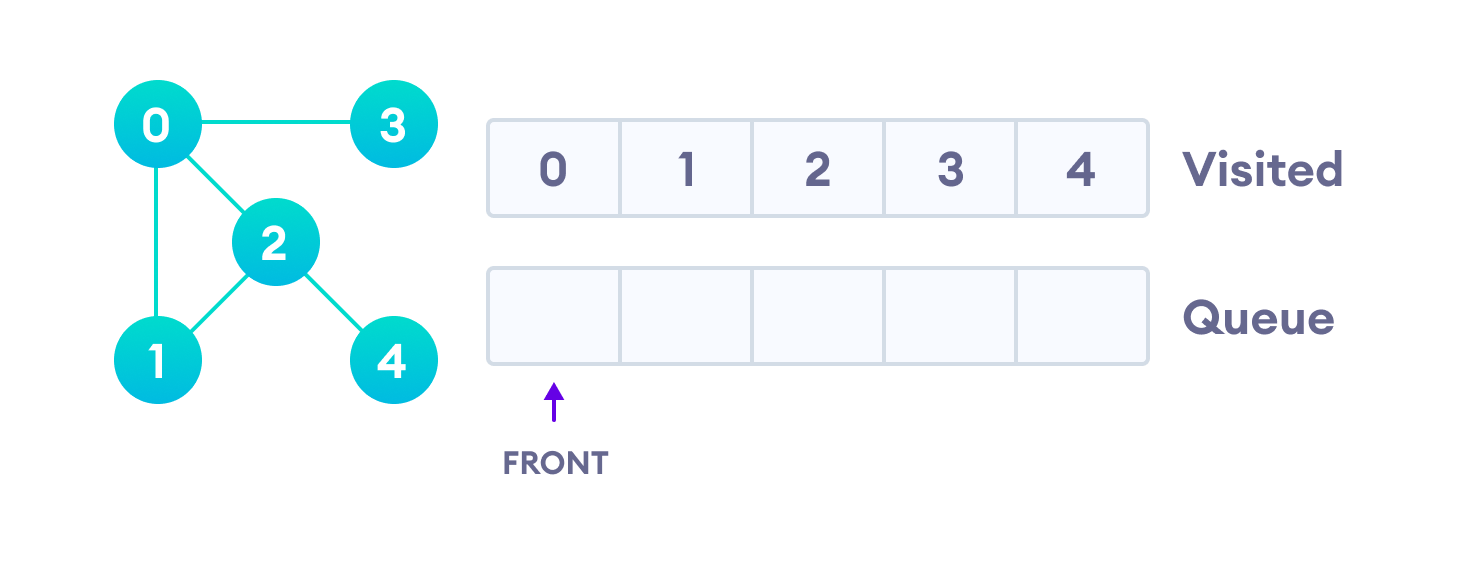
Quelle est l'ordre de parcours du graphe suivant en commençant par bleu ?

1. Parcours en profondeur (DFS)
2. Parcours en largeur (BFS)

Solution

Réponses possibles :

1. bleu - rouge - jaune - turquoise - orange - noir - vert
2. bleu - rouge - vert - jaune - turquoise - noir - orange

Notation polonaise inverse

Calculer les expressions suivantes en notation polonaise inverse , par exemple :

12 3 + 4 2 - * devient ( 12 + 3 ) * ( 4 - 2 ) = 15 * 2 = 30

1. 8 4 - 2 3 + /
2. 5 6 2 + * 8 4 / -
3. 7 3 + 2 5 + * 4 -
4. 10 2 3 * + 6 2 / -

Solution

1. ( 8 - 4 ) / ( 2 + 3 ) = 4 / 5 = 0.8
2. ( 5 * ( 6 + 2 ) ) - ( 8 / 4 ) = 40 - 2 = 38
3. ( ( 7 + 3 ) * ( 2 + 5 ) ) - 4 = 10 * 7 - 4 = 70 - 4 = 66
4. ( 10 + ( 2 * 3 ) ) - ( 6 / 2 ) = 10 + 6 - 3 = 16 - 3 = 13

Convertir les expressions suivantes de la notation polonaise inverse en expressions infixes, par exemple :

A B + C D - * devient ( A + B ) * ( C - D )

1. A B C - * D E + /
2. A B + C D + * E F - /
3. A B C * + D E F + / -
4. A B + C D - E F + * /

Solution

1. ( A * ( B - C ) ) / ( D + E )
2. ( ( A + B ) * ( C + D ) ) / ( E - F )
3. ( A + ( B * C ) ) - ( D / ( E + F ) )
4. ( ( A + B ) / ( C - D ) ) * ( E + F )

Convertir les expressions suivantes en notation polonaise inverse, par exemple :

( A + B ) * ( C - D ) devient A B + C D - *

1. ( A - B ) / ( C + D )
2. A * ( B + C ) - D / E
3. ( A + B ) * ( C + D ) / ( E - F )
4. A + B * C - D / ( E + F )

Solution

1. A B - C D + /
2. A B C + * D E / -
3. A B + C D + * E F - /
4. A B C * + D E F + / -

Références

• https://fr.wikipedia.org/wiki/Parcours_de_graphe
• https://fr.wikipedia.org/wiki/Algorithme_de_parcours_en_profondeur
• https://fr.wikipedia.org/wiki/Algorithme_de_parcours_en_largeur
• https://fr.wikipedia.org/wiki/Pile_(informatique)
• https://fr.wikipedia.org/wiki/File_(structure_de_donn%C3%A9es)
• https://fr.wikipedia.org/wiki/Notation_polonaise_inverse
• https://www.lecluse.fr/nsi/NSI_T/donnees/listes_piles_files/
• https://www.programiz.com/dsa/graph-dfs
• https://www.programiz.com/dsa/graph-bfs