Réseau de flot

Objectifs

• Définir le problème du flot maximum
• Appliquer l'algorithme de Ford-Fulkerson
• Définir une coupe dans un réseau de flot
• Connaître le théorème flot-max/coupe-min
• Trouver la coupe minimum d'un réseau de flot

Cours

Réseau de flot

Graphes

Problème du flot maximum

Trouver le flot maximum depuis une source vers un puits dans un graphe pondéré.

• Flot : quantité de matière qui circule dans un réseau.

• Source (S) : sommet d'où part le flot.

• Puits (T) : sommet où arrive le flot.

• Poids : capacité maximale d'un arc.

Problème du flot maximum

https://commons.wikimedia.org/wiki/File:Max_flow.svg

• Flot/Capacité : flot inférieur ou égal à la capacité de l'arc.

• A chaque sommet : flot entrant = flot sortant.

Réseau de distribution d'eau

https://www.circleofblue.org/2011/world/mixing-art-and-technology-north-americas-largest-membrane-filtration-sewage-plant-opens-near-seattle/attachment/pipes-and-puddles-655/

Réseau routier

https://www.rts.ch/info/suisse/13806396-le-conseil-federal-veut-plus-de-12-milliards-pour-le-reseau-routier.html

Réseau électrique

https://www.ifri.org/fr/espace-media/lifri-medias/de-transition-energetique-transformation-reseau-electrique

Algorithme de Ford-Fulkerson

https://www.programiz.com/dsa/ford-fulkerson-algorithm

Algorithme de Ford-Fulkerson

https://www.programiz.com/dsa/ford-fulkerson-algorithm

Initialisation des flots à 0.

Algorithme de Ford-Fulkerson

https://www.programiz.com/dsa/ford-fulkerson-algorithm

Recherche d'un chemin existant de S à T (DFS, BFS, ...).

Flot maximum du chemin : capacité minimale = 2

Algorithme de Ford-Fulkerson

https://www.programiz.com/dsa/ford-fulkerson-algorithm

Recherche d'un autre chemin existant de S à T.

Flot maximum du chemin : capacité minimale = 3

Algorithme de Ford-Fulkerson

https://www.programiz.com/dsa/ford-fulkerson-algorithm

Plus de chemin possible entre S et T : fin de l'algorithme.

Flot maximum : 2 + 3 = 5

Exercice

Solution

Flot maximum : 1 + 3 + 2 = 6

Solution

https://commons.wikimedia.org/wiki/File:FordFulkerson.gif

Coupe

https://commons.wikimedia.org/wiki/File:Min-cut.svg

• Coupe : ensemble d'arcs dont la suppression empêche le flot de passer de S à T.

• Sépare le graphe en deux sous-graphes.

• Capacité d'une coupe : somme des capacités des arcs de S à T.

Exercice : Capacité des coupes ?

https://www.hackerearth.com/practice/algorithms/graphs/min-cut/tutorial/

1. 15 + 10 = 25

2. 6 + 6 = 12

3. 4 + 6 + 6 = 16

4. 4 + 1 + 5 = 10

5. 10 + 5 = 15

Coupe minimum

• Coupe de capacité minimale d'un réseau de flot.

• Théorème flot-max/coupe-min

  • Capacité de la coupe minimum = Flot maximum

  • Pour vérifier la solution.

Théorème flot-max/coupe-min

https://commons.wikimedia.org/wiki/File:Max_flow.svg

• Flot maximum : 5

• Coupe minimale : {s, p} / {o, q, r, t} : 5

F pour passer en plein écran ou O pour afficher la vue d'ensemble.
Versions sans animation, plein écran, imprimable.

Exercices

Ford-Fulkerson

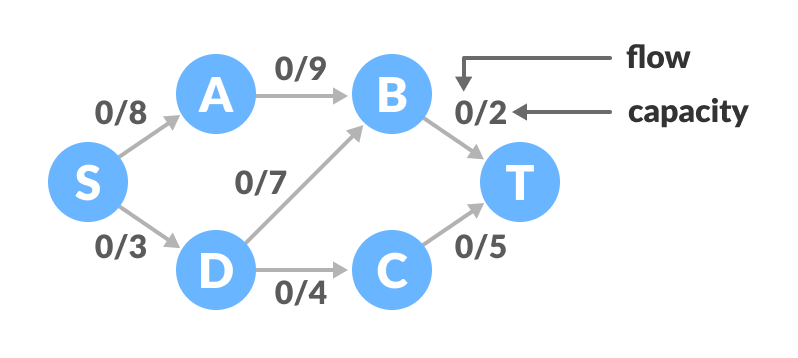
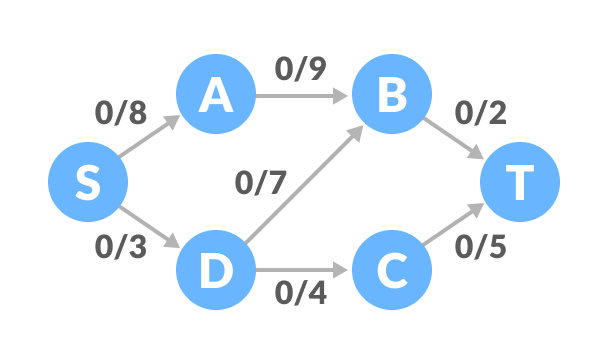
Appliquer l'algorithme de Ford-Fulkerson et trouver la coupe minimum sur les graphes suivants :

Solution

Flot maximum : 5 + 5 + 5 = 15

Coupe minimum : {S, U, V} / {T} ou {S} / {T, U, V}

Solution

Flot maximum : 2 + 3 + 2 = 7

Coupe minimum : {S, A} / {B, C, D, T} ou {S} / {A, B, C, D, T}

Références

• https://fr.wikipedia.org/wiki/R%C3%A9seau_de_flot
• https://fr.wikipedia.org/wiki/Probl%C3%A8me_de_flot_maximum
• https://www.programiz.com/dsa/ford-fulkerson-algorithm
• https://fr.wikipedia.org/wiki/Coupe_(th%C3%A9orie_des_graphes)
• https://www.hackerearth.com/practice/algorithms/graphs/min-cut/tutorial/
• https://fr.wikipedia.org/wiki/Coupe_minimum
• https://fr.wikipedia.org/wiki/Th%C3%A9or%C3%A8me_flot-max/coupe-min

Autres exemples

• https://www.scaler.com/topics/data-structures/ford-fulkerson-algorithm-for-maximum-flow-problem/