Théorie des graphes

Objectifs

• Définir les termes de base de la théorie des graphes
  • Graphe
  • Sommet
  • Arête
  • Arc
  • Boucle
  • Voisinage
  • Degré
  • Poids
  • Chaîne/Chemin
  • Cycle/Circuit
• Différencier graphe orienté et non orienté
• Reconnaître les différents topologies de graphes
• Modéliser un problème sous forme de graphe

Cours

Théorie des graphes

Graphes

Origine

https://commons.wikimedia.org/wiki/File:Konigsberg_bridges.png

• Problème des sept ponts de Königsberg

• Existe-t-il un chemin permettant de revenir à son point de départ en empruntant une seule fois chaque pont de la ville.

• Leonhard Euler (1735) : Prouve l'impossibilité de la solution grâce à la théorie des graphes.

Origine

https://commons.wikimedia.org/wiki/File:Konigsberg_bridges.png

https://commons.wikimedia.org/wiki/File:7_bridges.svg

https://commons.wikimedia.org/wiki/File:K%C3%B6nigsberg_graph.svg

Définitions

Graphe

• Un graphe comprend deux ensembles :

  • Ensemble de sommets

  • Ensemble d'arêtes/arcs reliant deux sommets

https://commons.wikimedia.org/wiki/File:Example_of_simple_undirected_graph.svg

Arêtes / arcs

• Arête

  • Graphe non orienté

  • L'arête ne possède pas de direction.

• Arc

  • Graphe orienté

  • L'arc possède une direction (flèche).

https://commons.wikimedia.org/wiki/File:Example_of_simple_directed_graph.svg

Voisinage & Degré

• Voisinage d'un sommet

  • Ensemble des sommets adjacents.

  • Graphes orientés : voisins entrants et sortants.

  • Exemple : Le voisinage de A est {A, B, C}.

• Degré d'un sommet

  • Nombre d'arêtes/arc connectés au sommet.

  • Degré entrant et sortant pour les graphes orientés.

  • Exemple : Le degré de A est 4.

https://commons.wikimedia.org/wiki/File:Example_of_simple_undirected_graph_2.svg

Boucle

• Boucle

  • Arête/arc reliant un sommet à lui-même.

https://commons.wikimedia.org/wiki/File:Example_of_simple_undirected_graph_with_loops.svg

Chaîne & Cycle

• Chaîne

  • Liste de sommets reliés par des arêtes.

  • Chemin pour les graphes orientés.

  • Exemple : H → A → B

• Cycle

  • Chaîne fermée (premier = dernier).

  • Circuit pour les graphes orientés.

  • Exemple : H → D → G → H

• Longueur d'une chaîne/cycle

  • Nombre d'arêtes/arcs.

https://commons.wikimedia.org/wiki/File:Graph_cycle.svg

Poids

• Poids d'une arête/arc

  • Valeur numérique associée à l'arête/arc.

  • Graphe pondéré si les arêtes/arcs possèdent des poids.

https://commons.wikimedia.org/wiki/File:Weighted_network.png

Utilisations

Calculer un itinéraire

https://www.mssqltips.com/sqlservertip/8255/graph-theory-shortest-path-algorithms/

Graphe social

https://www.macg.co/news/voir/217362/facebook-devoile-un-nouveau-profil-et-un-nouveau-graphe-social

Chaîne de Markov

https://commons.wikimedia.org/wiki/File:Markov_Chain_weather_model_matrix_as_a_graph.png

Topologie

https://commons.wikimedia.org/wiki/File:Topologies_de_r%C3%A9seaux.png

1. homogène : régulier (distribué)

2. hiérarchique : arbre

3. cyclique : revient à lui-même

4. centralisé ou polaire : étoile

5. quelconque : autres

Exercice

https://commons.wikimedia.org/wiki/File:6n-graph2.svg

• Graphe pondéré ?

  • Non

• Graphe orienté ?

  • Non

Exercice

https://commons.wikimedia.org/wiki/File:Weighted_network.png

• Combien de sommets ?

  • 10

• Combien d'arcs ?

  • 0

• Combien d'arêtes ?

  • 12

Exercice

https://www.bibmath.net/ressources/index.php?action=affiche&quoi=bde/graphes/graphes_pratiques&type=fexo

• Lesquels représentent le même graphe ?

  • Les deux premiers

F pour passer en plein écran ou O pour afficher la vue d'ensemble.
Versions sans animation, plein écran, imprimable.

Exercices

Terminologie

Compléter le tableau avec les définitions des termes suivants :

• Arc
• Arête
• Boucle
• Chaîne
• Chemin
• Circuit
• Cycle
• Degré
• Graphe
• Longueur
• Poids
• Sommet
• Voisinage

Graphe non orienté	Graphe orienté	Description
Sommet	Sommet	Représente un objet ou une entité.
Arête	Arc	Relie deux sommets.
...

Solution

Graphe non orienté	Graphe orienté	Description
Sommet	Sommet	Représente un objet ou une entité.
Arête	Arc	Relie deux sommets.
Boucle	Boucle	Relie un sommet à lui-même.
Voisinage	Voisinage	Ensemble des sommets adjacents.
Degré	Degré	Nombre d'arêtes/arc connectées.
Poids	Poids	Valeur associée à une arête/arc.
Chaîne	Chemin	Suite de sommets reliés par des arêtes/arcs.
Cycle	Circuit	Chaîne/chemin qui commence et finit au même sommet.
Longueur	Longueur	Nombre d'arêtes/arcs dans une chaîne/chemin.

Caractéristiques d'un graphe

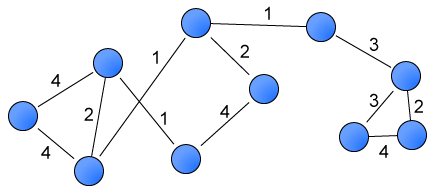
Donner les caractéristiques du graphe ci-dessus :

1. Graphe orienté ou non orienté ?
2. Graphe pondéré ou non pondéré ?
3. Nombre de sommets ?
4. Nombre d'arêtes ?
5. A une boucle ?
6. A un cycle ?
7. Quel est le degré du sommet b ?
8. Quel est le voisinage du sommet c ?
9. Quelle est la longueur de la chaîne a → c → d ?
10. Quel est le poids de la chaîne a → c → d ?
11. Quel est le chemin le plus court (chaîne de poids minimal) entre a et d ?

Solution

1. Graphe non orienté
2. Graphe pondéré
3. 4 sommets
4. 5 arêtes
5. Pas de boucle
6. Cycle, par exemple a → b → c → a
7. 3
8. a, b et d
9. 2
10. 7
11. a → b → d

Modélisation chemin de fer

Pour se rendre à Zürich depuis Lausanne, les trains suivants sont disponibles :

• Direct :
  • Lausanne → Zürich
• Correspondance avec un changement :
  • Lausanne → Berne → Zürich
  • Lausanne → Bâle → Zürich
• Correspondance avec deux changements :
  • Lausanne → Berne → Olten → Zürich
  • Lausanne → Bâle → Olten → Zürich

Modéliser ces différents trajets sous forme de graphe orienté.

Solution

Topologies de graphes

Pour chaque graphe, indiquer quelles sont leurs topologies parmi :

• Homogène
• Hiérarchique
• Cyclique
• Centralisé
• Quelconque

Solution

• Homogène
• Cyclique

Solution

• Hiérarchique

Solution

• Hiérarchique
• Centralisé

Modélisation musée

Voici le plan du musée archéologique d'Olympie :

Modéliser ce plan sous forme de graphe.
Que représente chaque sommet et chaque arête ?

Solution

Modélisation interactions sociales

Modéliser les interactions entre les personnes suivantes sous forme de graphe :

• Anna est amie avec Bob, Céline et Emile
• Céline est amie avec Bob et François
• Guillaume est ami avec Hector, François et Anna

1. Serait-ce plutôt un graphe orienté ou non orienté ? Pourquoi ?
2. Que représente chaque sommet et chaque arête ?
3. Que pourrait signifier une pondération du graphe ?

Solution

1. Non orienté, car l'amitié est réciproque.
2. Chaque sommet représente une personne et chaque arête représente une amitié.
3. Le poids d'une arête pourrait représenter la proximité entre deux personnes (nombre de centres d'intérêts en commun par exemple).

Références

• https://fr.vikidia.org/wiki/Graphe_(th%C3%A9orie_des_graphes)
• https://fr.wikipedia.org/wiki/Th%C3%A9orie_des_graphes
• https://fr.wikipedia.org/wiki/Graphe_(math%C3%A9matiques_discr%C3%A8tes)
• https://fr.wikipedia.org/wiki/Probl%C3%A8me_des_sept_ponts_de_K%C3%B6nigsberg