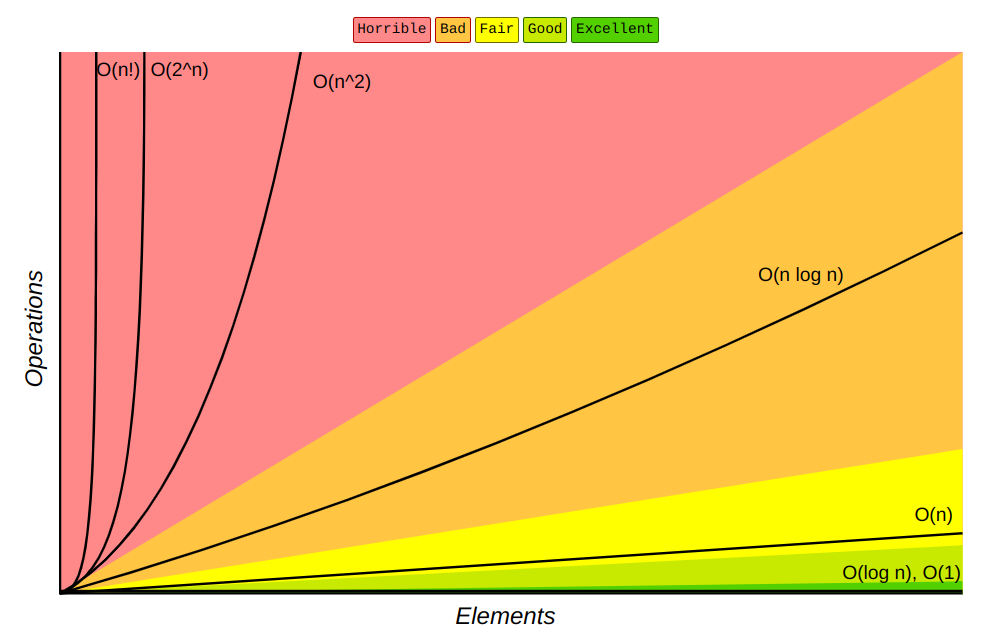
Complexité
Objectifs
Comment comparer des algorithmes ?
- Différencier complexité en temps et en espace
- Estimer la complexité d'un algorithme
Cours
Complexité
AlgorithmiqueComplexité
Recettes pour une omelette
Recettes pour une omelette
Complexité algorithmique
Complexité algorithmique
Mesurer l'efficacité d'un algorithme
En temps (opérations effectuées)
1 opération = 1 unité de temps
1 opération = 1 comparaison, 1 addition, 1 affectation, ou …
En espace (espaces dans la mémoire utilisés)
1 variable = 1 espace
1 liste de n élément = n espaces
Notation grand O de Landau
Ordre de grandeur selon des entrées possibles
Multiplication
Multiplication
FONCTION mult(a, b)
RETOURNER a*b
FIN FONCTION
Instance : a=3, b=4
Opérations
2 (mult. + retour)
Espaces
2 (variables a et b)
Instance : a=2048, b=130
Opérations
2
Espaces
2
Complexité temporelle : constante O(1)
Complexité spatiale : constante O(1)
Multiplication
Multiplication
FONCTION mult(a, b)
r ← 0
POUR i DE 1 À b FAIRE
r ← r + a
FIN POUR
RETOURNER r
FIN FONCTION
Instance : a=3, b=4
Opérations
4 (assign. + add.)
Espaces
4 (var. a, b, r, i)
Instance : a=2048, b=130
Opérations
130
Espaces
4
Complexité temporelle : linéaire O(b) ou O(n)
Complexité spatiale : constante O(1)
Grand O de Landau
Grand O de Landau
O(1) : Constant (min, max)
O(log(n)) : Logarithmique (recherche dichotomique)
O(n) : Linéaire (recherche dans liste)
O(n log(n)) : Log-linéaire (tri fusion)
O(n2) : Quadratique (tri par insertion/sélection)
2O(n) : Exponentiel
O(n!) : Factorielle
n | O(1) | O(n) | O(n2) |
|---|---|---|---|
1 | 1 | 1 | 1 |
10 | 1 | 10 | 100 |
100 | 1 | 100 | 10000 |
1000 | 1 | 1000 | 1000000 |
… | … | … | … |
Grand O de Landau
Grand O de Landau
https://www.sfeir.dev/front/comprendre-la-complexite-des-algorithmes/
Exercice
Exercice
FONCTION max(a, b)
SI a < b
RETOURNER b
SINON
RETOURNER a
FIN SI
FIN FONCTION
Complexité temporelle
O(1)
Complexité spatiale
O(1)
Exercice
Exercice
FONCTION factorielle(n)
r ← 1
POUR i DE 1 À n FAIRE
r ← r*i
FIN POUR
RETOURNER r
FIN FONCTION
Complexité temporelle
O(n)
Complexité spatiale
O(1)
Versions sans animation, plein écran, imprimable.
Exercices
Calculer la complexité temporelle et spatiale des algorithmes suivants.
Max
FONCTION max(a, b)
SI a < b ALORS
RETOURNER b
SINON
RETOURNER a
FIN SI
FIN FONCTION
Solution
- Temps : O(1) car il n'y a pas de boucle, on effectue un nombre constant d'opérations.
- Espace : O(1) car il n'y a pas de liste qui grandit avec la taille des entrées.
Max Liste
FONCTION max_liste(liste)
max ← liste[0]
POUR i DE 1 À liste.taille - 1 FAIRE
SI liste[i] > max ALORS
max ← liste[i]
FIN SI
FIN POUR
RETOURNER max
FIN FONCTION
Solution
- Temps : O(n) car on parcourt une boucle qui dépend de la taille de la liste.
- Espace : O(n) car il y a une liste qui grandit avec la taille des entrées.
Recherche
FONCTION recherche(liste, valeur)
i ← 0
TANT QUE i < liste.taille FAIRE
SI liste[i] = valeur ALORS
RETOURNER i
FIN SI
i ← i + 1
FIN TANT QUE
RETOURNER -1
FIN FONCTION
Solution
- Temps : O(n) car on parcourt potentiellement toute la liste.
- Espace : O(n) car il y a une liste qui grandit avec la taille des entrées.
Inverse
FONCTION inverse(liste)
liste_inverse ← liste
POUR i DE 1 À liste.taille FAIRE
liste_inverse[i - 1] ← liste[liste.taille - i]
FIN POUR
RETOURNER liste_inverse
FIN FONCTION
Solution
- Temps : O(n) car on parcourt une boucle qui dépend de la taille de la liste.
- Espace : O(n) car il y a une liste qui grandit avec la taille des entrées.